Intervals
The ratio in pitch between two notes is called an interval. Intervals can also be thought of in terms of the number of steps that exist between two notes. The smallest interval is called a unison. It occurs when two of the exact same pitches are played (no steps). It is possible to play harmonic unisons on the guitar, while it is not possible to play harmonic unisons on the piano. The next larger interval is known as a half step or semitone. On the guitar a semitone above a note is simply one fret higher on the same string. The next higher interval beyond a semitone, is the whole step.
It is possible to classify intervals in terms of the number of steps they contain, however, when dealing with note names or sheet music notation, it is necessary to provide two names that quantify the exact interval. These two names are generally referred to as the specific and general interval names.
General interval names are calculated by counting the number of note names inclusive. For example, C to G is a "Fifth", (C-D-E-F-G), since there are 5 names inclusive that comprise the interval. The letter names rollover after G, so F to B is a "fourth", (F-G-A-B). The general interval name is easy to calculate.
The specific interval, on the other hand, is more difficult to calculate. Specific intervals are calculated by constructing a Major scale on the lower note and determining how many steps the upper note differs from the Major scale note that would fall on that line or space. This is a time consuming practice, and later in this chapter we will describe a way to memorize all of the intervals so that you don't have to construct a Major scale each time. The naming process also depends on the general interval name, general intervals of 1, 4, 5, 8 and general intervals of 2, 3, 6 and 7 form two distinct naming conventions shown below:
|
Interval versus Implied Major Scale Note |
1 (unison) |
2 (second) |
|
4 (fourth) |
3 (third) |
|
|
5 (fifth) |
6 (sixth) |
|
|
8 (octave) |
7 (seventh) |
|
| If the upper note lies one half step above the implied major scale note: |
Augmented (Aug) |
Augmented (Aug) |
| If the upper note lies exactly on the implied major scale note: |
Perfect (P) |
Major (Maj) |
| If the upper note lies one half step below the implied major scale note: |
diminished (dim) |
minor (min) |
| If the upper note lies one whole step below the implied major scale note: |
(doubly diminished) |
diminished (dim) |
We often use P for Perfect, A for Augmented, M for Major, m for minor, and d for diminished. Any intervals larger than augmented become doubly, triply or quadruply augmented, and intervals smaller than diminished become double, triply or quadruply diminished. These types of intervals are extremely rare.
Example 1: D up to E (which spans two half steps)
This interval is some type of second (D-E spans two note names inclusive). Constructing the Major scale yields D, E, F sharp, G, A, B, C sharp, D. Looking at the right side of the previous table under the 2nds, 3rds, 6ths and 7ths column, since the upper note falls exactly on the implied Major scale note, the interval is a "Major" interval. The full name becomes "Major 2nd".
Example 2: D up to F flat (which still spans two half steps)
This interval is a 3rd, since D-E-F spans three letter names. A major scale constructed on top of D starts out as D-E-F sharp-G... Since the F flat is two half steps below the note F sharp that would fall in the major scale, from the right hand side of the above table under the 2nds, 3rds, 6ths and 7ths column, stepping down two rows from Major yields diminished, therefore the interval is a diminished 3rd.
Calculating intervals by constructing a major scale is a painstaking process that takes you a considerable amount of time. If you can image what the key signature would be for a major scale built on the lower note, you can save yourself some time if you can visualize if the upper note would lie within the key signature of the lower note.
Example 3: A up to D flat
Counting letter names, A-B-C-D, this interval is some type of fourth. Remember from the circle of fifths that this key signature for A Major contains 3 sharps and from the circle of fifths natural ordered set (F, C, G, D, A, E, B), that the natural notes that get sharpened are the first three of these notes starting from the left (F sharp, C sharp, G sharp). From this, we can determine that D is not in the key signature (not included in F sharp, C sharp or G sharp). Therefore, D is natural in the key of A. The upper note, D flat then is one half step smaller, so looking at the left side of the previous table under the 1sts, 4ths, 5ths, 8ths column, stepping down one row from Perfect yields diminished, therefore the interval is a diminished 4th.
This would be a nice way to calculate the interval names, however there are some problems. First, you have to know the circle of fifths and the number of accidentals in all key signatures very thoroughly. Also, since there are 15 different key signatures, (C flat, G flat, D flat, A flat, E flat, B flat, F, C, G, D, A, E, B, F sharp and C sharp) and 21 different possible note names (not including double sharps or flats), ( C, D, E, F, G, A, B all with either sharp, flat or natural signs), there are some starting notes that we never calculate key signatures and therefore starting notes with. The reason for this is that you start obtaining double flats and double sharps within the Major scale built on notes that are not in the list of 15 key signatures, with all 7 notes already sharpened or flattened in C flat and C sharp Major, something has to give.
Therefore, if you do come upon a lower note that is not one of the 15 key signature Major tonics, you can simply make that note natural, by either sharpening it or flattening it, use the key signature for that new note, sharpen or flatten the upper note in the same way that you altered the lower note and check if the altered upper note exists in the new key signature. You still have to count the gap in the notes in order to know the general interval name.
For example, D sharp up to B. Since D sharp is not one of the 15 tonic notes of the Major key signatures, flatten it to become D natural, you must also flatten the upper note, which now becomes B flat. The key signature for D contains two sharps, F sharp and C sharp, meaning that B would be a natural in that key. Since B flat lies one half step below the 6th note in a Major scale built upon D, the interval is named (from the right side of the previous table) minor 6th.
The same technique can be used for naming intervals that start with double flats or double sharps as well. For example, F double flat to G. Key signatures never contain double flats or double sharps, so sharpen F double flat twice to get F, sharpen G twice to get G double sharp. The key signature for F has one flat, B flat, therefore G will be natural in the key of F. Since G double sharp is two half steps above the implied Major scale note, from the right side of the previous table, we see that it is one step higher than an Augmented interval, it therefore is double Augmented.
The following table lists the names of the most common intervals by number of half steps in the interval.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
P1 |
m2 |
M2 |
m3 |
M3 |
P4 |
d5 |
P5 |
m6 |
M6 |
m7 |
M7 |
P8 |
|
d2 |
A1 |
d3 |
A2 |
d4 |
A3 |
A4 |
d6 |
A5 |
d7 |
A6 |
d8 |
A7 |
Intervals that span no more than an octave are known as simple intervals. Intervals that span more than an octave are known as compound intervals. Compound intervals are more easily identified by shifting the upper note of the interval down by octaves until it lies within an octave of the lower note. The interval is then named according to any of the previously demonstrated methods. After calculating the specific name, the general name is then calculated by adding back the number of scale degrees that were deleted in the downward shift process. Interval general names are usually constrained to lie within two octaves, i.e., the general name is usually less than or equal to a 15th.
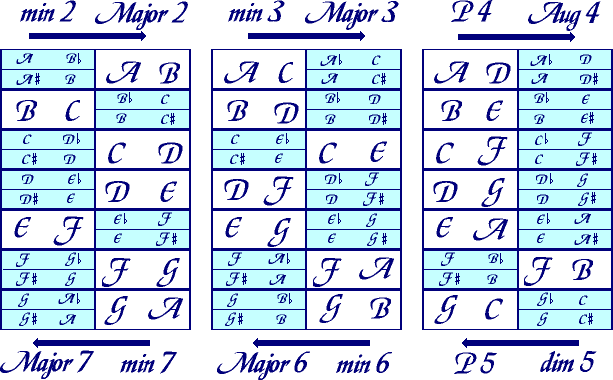
Fortunately, there is a much quicker way to name intervals, which is similar to using multiplication tables in math, so that you don't have to "add things" up. Simply memorize the large letters in the following three tables or the bullet list below the tables, so that you can automatically name both the general and specific portions of the interval name without counting. (The light blue rows give a more complete view of some of the possible name combinations that make up intervals.)
Interval Name Tables
(Copyright 1992 RubyCliff Computing):

|
The important things to remember are:
|
These tables can be so concisely written due to the ability to invert intervals, described later in this chapter. The meaning of these tables is as follows:
For two notes that you want to calculate a complete interval name for, find the two note names in some box in the above tables. For example, lets try to find the interval name of a C up to a D.
In the leftmost table, the interval between a C up to a D can be found in the second column, third row. Since you found the notes listed left to right in the table, you use the name of the interval above the table with the arrow pointing left to right. This interval corresponds to a Major 2nd. Calculating the name of an interval with a low D up to a C, (going right to left in the table), minor 7th, requires looking at the name at the bottom of the table underneath that column with the arrow pointing right to left.
All of the intervals on the right side of the leftmost table, (A to B, C to D, D to E, F to G, G to A) are Major 2nds. The intervals on the left side of this table, (B to C, E to F) are minor 2nds, going left to right. Conversely, all of the intervals on the right side of the table are minor 7ths and all of the intervals on the left side of the table are Major 7ths looking right to left.
How about A flat to G sharp? This is clearly not in the table. The closest entry is Major 7th on the bottom row of the leftmost table, A flat to G. Since our interval has a top note that is higher than the top note from this entry, our interval is expanded. Therefore, knowing that an Augmented interval is larger than a Major interval, our interval becomes an Augmented 7th.
The tables are invaluable in immediately providing the full interval name for any two given notes. For example, a G up to an E is a Major 6th, calculating manually requires you to count G, A, B, C, D, E to come up with the general name of 6th. After calculating a general name, you must then determine if the E should be sharp, natural or flat to fit in the Major scale or via the key signature, so that you can call it Augmented, Major, minor or diminished. Since you can simply memorize the natural intervals that make up the table, you automatically know that G up to E is a Major 6th without requiring any calculations.
What about a Perfect 5th starting on G? How would you calculate the upper note of that Interval? Go to the rightmost table and look for P5 on the bottom of the table, it signifies that you must go from Right to Left to get the second note. That note is D. You should already know all of the fifths and fourths from the circle of fifths however.
The interval name tables rely on what is known as the "inversion of intervals". Intervals may be inverted by taking the lower note and moving it an octave higher, or by taking the upper note of an interval and moving it an octave lower. The result of inverting a 1st (unison) is an 8th (octave), the result of inverting a 2nd is a 7th. The original general interval and the inverted general interval numbers add up to the number nine. This is why a column in that table can have two meanings (e.g., Major 2nd or minor 7th) depending on the direction of travel between the two notes, (left to right or right to left).
|
1st |
inverts to and from |
8th |
|
2nd |
inverts to and from |
7th |
|
3rd |
inverts to and from |
6th |
|
4th |
inverts to and from |
5th |
The specific interval names, transform Perfect to Perfect (e.g., P4 inverted becomes P5), Augmented to diminished, Major to minor.
|
Perfect |
inverts to and from |
Perfect |
|
Augmented |
inverts to and from |
diminished |
|
Major |
inverts to and from |
minor |
Examples:
An example from the table:
Intervals on the guitar take on distinctive shapes depending on whether or not the interval crosses the boundary between the second and third string, here marked with a red line. This boundary is created due to the fact that there is a Major 3rd between the second and third strings, and a Perfect fourth between all of the other pairs of consecutive strings. This interval is a unison, or (Perfect 1st). This interval is commonly used on the guitar in order to tune the strings to each other.

All other octave bound intervals are listed in the Appendix under Interval Fret Table.
Now that you have a basic understanding of intervals, you are ready to learn about chords.